Hi @inseo, and welcome to the forum!
I think that you have two questions in this post:
What is the expected data rates at different downsampling frequencies?
The raw JLS storage at 2 MSPS is very efficient since it stores just 32 bits per sample. In contrast, downsample data must store three 32-bit floating-point values (current, voltage, power) and three 8-bit values (current_range, current_lsb, voltage_lsb), which increases the storage size by a factor of 3.75. You were very precise in your data rate measurements, which almost exactly match the 3.75 factor!
2000 kHz → 470 MB (accept as the baseline, but I would expect closer to 486 MB)
1000 kHz → 881 MB
500 kHz → 441 MB
200 kHz → 176 MB
100 kHz → 88 MB
We have been investigating a bounded lossy compression algorithm that will help significantly reduce the downsampled size. We have also considered adding a signal selection to store the signals you want.
What happens when I downsample a signal?
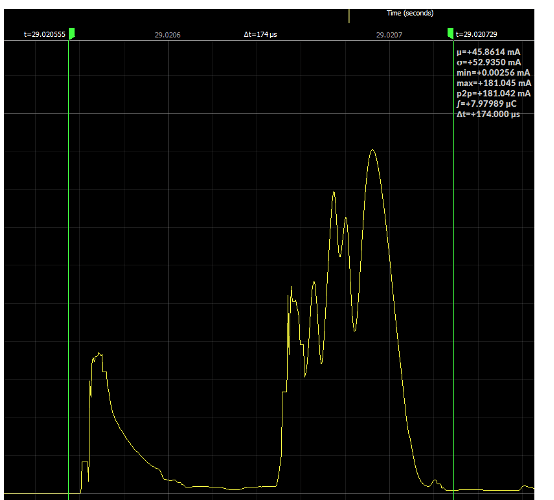
To accurately downsample a signal, it must first be low-pass filtered to reduce the bandwidth to 1/2 of the output downsampled sampling frequency (see Nyquist-Shannon sampling theorem). Low-pass filtering prevents aliasing and correctly maintains the mean, which is often very important for Joulescope applications. The filter reduces the signal bandwidth. Sharp edges, as shown in your capture, have high-frequency content. As those edges are filtered, they become poorly approximated, which causes overshoot. All About Circuits has an excellent description in this Square Wave Signals article. Although your captured input signal is not a square wave, any sharp edge has this square wave effect. The good news is that the mean is accurately maintained. The bad news is that you lose time resolution, but reduced time resolution is the purpose of downsampling.
With filter, you also need to ask the question of how much the energy is “smeared.” The Joulescope downsampling implementation uses FIR filters, which you can find here. The 50 ksps filter has a duration of 130 / 4 samples at 50 kHz = 650 µs. The “smearing” effect makes easily and accurately comparing energy between events a little tricky unless the events are separated by at least that duration.
Did I correctly understand and answer your questions?